
Hence we must divide the coordinate difference by 8. Now that we have them, let’s define the width and height of a box: boxwidth = (bottomrightx - topleftx)/8 boxheight = (bottomrighty - toplefty)/8Įxplanation: when looking at a row of cells, the distance from the leftmost to the rightmost cell is 8 box widths. In my case the numbers were: topleftx = 975 toplefty = 507 bottomrightx = 1307 bottomrighty = 846 Now let’s define the pixel coordinates of two cells on our puzzle: top-left and bottom-right. Since we are not going to use our previous sudoku array, let’s change all the numbers in this array to zero: sudoku =, ,, ,, ,, , ] To get the locations of all the numbers, use the following: for i in range(1, 10): for pos in pag.locateAllOnScreen(str(i)+'.png'): print(pos) Filling the sudoku array The third and fourth give us the dimensions of our image but at the moment we are not going to need them. The first two parameters (left and top) give us the pixel coordinates of the top-left corner of our image. Returns all locations of number three on our screen: Box(left=1124, top=510, width=32, height=33) Box(left=959, top=845, width=32, height=33) In my case for pos in pag.locateOnScreen("3.png"): print(pos) The PyAutoGUI module has a function that locates the given image on your screen. Let’s name them as “1.png”, “2.png”, etc. The snippets may have different dimensions, as long as they all feature only a number on a white background. If our assumption was incorrect then the 9-th line would return False and that sets the value of a cell in i-th row and j-th column to zero. If the entry is valid (verified by the isValid function) then tries to solve the sudoku recursively under the assumption that this is a correct entry. If there is an empty cell at i-th row and j-th column then it will try to fit all the possible entries from 1 to 9 into this box. If i is equal to -1 then we have completed solving our puzzle. The first three lines of the function make sure that we have an empty cell in our puzzle. We’ll do it with the following function: def solveSudoku(sudoku, i=0, j=0): i, j = findNextCellToFill(sudoku) if i = -1: return True for e in range(1, 10): if isValid(sudoku, i, j, e): sudoku = e if solveSudoku(sudoku, i, j): return True sudoku = 0 return False Now it’s all about solving the given sudoku.

Otherwise, the function will return False. The following function returns True if none of the three rules are violated. We need a function that checks whether it violates the three main rules of sudoku when placed to the i-th row and j-th column. Whenever it encounters an empty cell, the function returns the corresponding indexes. This iterates through all the columns in the first row, then second row and so on. def findNextCellToFill(sudoku): for x in range(9): for y in range(9): if sudoku = 0: return x, y return -1, -1 To solve a certain cell, we must first find the row and column number of a cell that’s empty. Yet, it’s licensed as Creative Commons BY-NC-SA which gives me a green light for sharing.

The idea and implementation were copied from MIT OpenCourseWare Youtube channel, more specifically from this video. Let’s get to it! Now we are ready for a step-by-step algorithm-creation.ĭisclaimer: I did not create this sudoku-solving algorithm entirely myself. def printsudoku(): print("\n\n\n\n\n") for i in range(len(sudoku)): line = "" if i = 3 or i = 6: print("-") for j in range(len(sudoku)): if j = 3 or j = 6: line += "| " line += str(sudoku)+" " print(line)Īn example output of a printsudoku function
#Sudoku rules code#
Below is the code example along with its output. Hence, it would be great to print out the current state of the puzzle. Sure, this two-dimensional python array does not look like real sudoku without any gridlines.
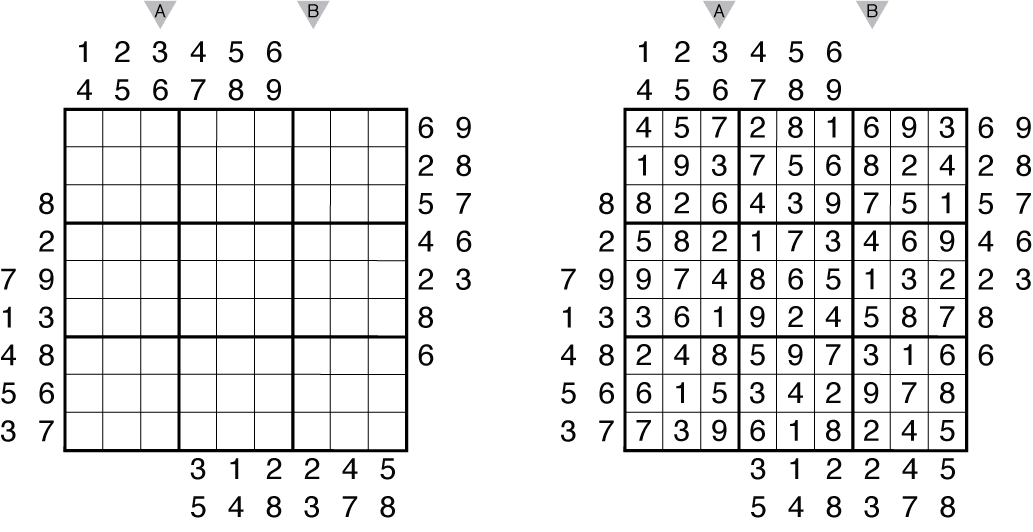
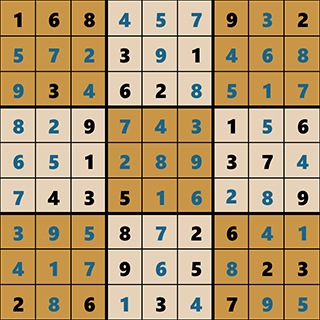
When trying to access a certain element from the i-th row and j-th column, you simply need to call sudoku Making it look a lot more like a real sudoku We should obtain the following: sudoku =, ,, ,, ,, , ] I propose that we handle this puzzle as a two-dimensional Python array where empty boxes are represented with zeros and other boxes with corresponding numbers. Let’s take a random sudoku puzzle from the Internet and try to solve it with Python.


 0 kommentar(er)
0 kommentar(er)
